Ordinal analysis

In proof theory, ordinal analysis assigns ordinals (often large countable ordinals) to mathematical theories as a measure of their strength. The field was formed when Gerhard Gentzen in 1934 used cut elimination to prove, in modern terms, that the proof theoretic ordinal of Peano arithmetic is ε₀.

1 Definition
2 Examples
3 See also
4 References

Definition

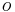Ordinal analysis concerns true, effective (recursive) theories that can interpret a sufficient portion of arithmetic to make statements about ordinal notations. The proof theoretic ordinal of such a theory $T$ is the smallest recursive ordinal that the theory cannot prove is well founded — the supremum of all ordinals $\alpha$ for which there exists a notation $o$ in Kleene's sense such that $T$ proves that 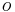$o$ is an ordinal notation. Equivalently, it is the supremum of all ordinals $\alpha$ such that there exists a recursive relation $R$ on $\omega$ (the set of natural numbers) which well-orders it with ordinal $\alpha$ and such that $T$ proves transfinite induction of arithmetical statements for $R$ .

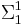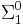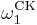The existence of any recursive ordinal which the theory fails to prove is well ordered follows from the $\Sigma^1_1$ bounding theorem, as the set of natural numbers which an effective theory proves to be ordinal notations is a $\Sigma^0_1$ set (see Hyperarithmetical theory). Thus the proof theoretic ordinal of a theory will always be a countable ordinal less than the Church-Kleene ordinal $\omega_1^{\mathrm{CK}}$ .

In practice, the proof theoretic ordinal of a theory is a good measure of the strength of a theory. If theories have the same proof theoretic ordinal they are often equiconsistent, and if one theory has a larger proof theoretic ordinal than another it can often prove the consistency of the second theory.

Examples

Theories with proof theoretic ordinal ω²

RFA, rudimentary function arithmetic.
IΔ₀, arithmetic with induction on Δ₀-predicates without any axiom asserting that exponentiation is total.

Theories with proof theoretic ordinal ω³

Friedman's grand conjecture suggests that much "ordinary" mathematics can be proved in weak systems having this as their proof-theoretic ordinal.

EFA, elementary function arithmetic.
IΔ₀ + exp, arithmetic with induction on Δ₀-predicates augmented by an axiom asserting that exponentiation is total.
RCA*
0, a second order form of EFA sometimes used in reverse mathematics.
WKL*
0, a second order form of EFA sometimes used in reverse mathematics.

Theories with proof theoretic ordinal ωⁿ

IΔ₀ or EFA augmented by an axiom ensuring that each element of the n-th level 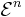$\mathcal{E}^n$ of the Grzegorczyk hierarchy is total.

Theories with proof theoretic ordinal ω^ω

RCA₀, recursive comprehension.
WKL₀, weak König's lemma.
PRA, primitive recursive arithmetic.
IΣ₁, arithmetic with induction on Σ₁-predicates.

Theories with proof theoretic ordinal ε₀

PA, Peano arithmetic (shown by Gentzen using cut elimination).
ACA₀, arithmetical comprehension.

Theories with proof theoretic ordinal the Feferman-Schütte ordinal Γ₀

This ordinal is sometimes considered to be the upper limit for "predicative" theories.

ATR₀, arithmetical transfinite recursion.
Martin-Löf type theory.

Theories with proof theoretic ordinal the Bachmann-Howard ordinal

ID₁, the theory of inductive definitions.
KP, Kripke-Platek set theory with the axiom of infinity.
CZF, Aczel's constructive Zermelo-Fraenkel set theory.

Theories with larger proof theoretic ordinals

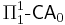$\Pi^1_1\mbox{-}\mathsf{CA}_0$ , Π₁¹ comprehension has a rather large proof theoretic ordinal, which was described by Takeuti in terms of "ordinal diagrams", and which is bounded by ψ₀(Ω_ω) in Buchholz's notation. It is also the ordinal of 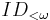$ID_{<\omega}$ , the theory of finitely iterated inductive definitions.
KPM, an extension of Kripke-Platek set theory based on a Mahlo cardinal, has a very large proof theoretic ordinal, which was described by Rathjen (1990).

Most theories capable of describing the power set of the natural numbers have proof theoretic ordinals that are (as of 2008^[update]) so large that no explicit combinatorial description has yet been given. This includes second order arithmetic and set theories with powersets. (Kripke-Platek set theory mentioned above is a weak set theory without power sets.)

References

Buchholz, W.; Feferman, S.; Pohlers, W.; Sieg, W. (1981), Iterated inductive definitions and sub-systems of analysis, Lecture Notes in Math., 897, Berlin: Springer-Verlag, doi:10.1007/BFb0091894, ISBN 978-3-540-11170-2
Pohlers, Wolfram (1989), Proof theory, Lecture Notes in Mathematics, 1407, Berlin: Springer-Verlag, ISBN 3-540-51842-8, MR 1026933
Pohlers, Wolfram (1998), Set Theory and Second Order Number Theory, "Handbook of Proof Theory", Handbook of Proof Theory, Studies in Logic and the Foundations of Mathematics (Amsterdam: Elsevier Science B. V.) 137: pp. 210–335, ISBN 0-444-89840-9, MR 1640328
Rathjen, Michael (1990), "Ordinal notations based on a weakly Mahlo cardinal.", Arch. Math. Logic 29 (4): 249–263, doi:10.1007/BF01651328, MR 1062729
Rathjen, Michael (2006), "The art of ordinal analysis", International Congress of Mathematicians, II, Zürich,: Eur. Math. Soc., pp. 45–69, MR 2275588, http://www.icm2006.org/proceedings/Vol_II/contents/ICM_Vol_2_03.pdf
Rose, H. (1984), Subrecursion. Functions and Hierarchies, Oxford logic guides, 9, Oxford, New York: Clarendon Press, Oxford University Press
Schütte, Kurt (1977), Proof theory, Grundlehren der Mathematischen Wissenschaften, 225, Berlin-New York: Springer-Verlag, pp. xii+299, ISBN 3-540-07911-4, MR 0505313
Takeuti, Gaisi (1987), Proof theory, Studies in Logic and the Foundations of Mathematics, 81 (Second ed.), Amsterdam: North-Holland Publishing Co., ISBN 0-444-87943-9, MR 0882549

Ordinal analysis

Contents

Definition

Examples

Theories with proof theoretic ordinal ω2

Theories with proof theoretic ordinal ω3

Theories with proof theoretic ordinal ωn

Theories with proof theoretic ordinal ωω

Theories with proof theoretic ordinal ε0

Theories with proof theoretic ordinal the Feferman-Schütte ordinal Γ0